Tilsyneladende dybde

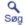
Forsøg nr.: 115
Formål: At demonstrere tilsyneladende dybde. At finde brydningsindeks for en væske.
Resume: En genstand lægges på bunden af et glas vand, som placeres på en overheadprojektor. Billedet fokuseres på skærmen. En blyant køres op langs siden af glasset, indtil også den er i fokus. Placeringen af blyanten kan bruges til at udregne vandets brydningsindeks.
Nøgleord: Brydning, brydningsindeks, lys, optik.

Beskrivelse:

Når en lysstråle passerer en grænseoverflade mellem vand og luft, vil den afbøjes i en vinkel, der er bestemt af Snells Lov. For en genstand (f.eks. en mønt), der ligger på bunden af et vandkar, betyder dette, at en observatør vil opfatte mønten som liggende på en "tilsyneladende dybde", der er mindre end den faktiske dybde: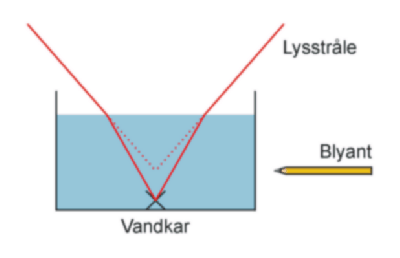

Lys, der rammer en vandoverflade, vil brydes og afbøjes. Derved kommer en genstand, der ligger på bunden af glasset, til at have en tilsyneladende dybde, der er mindre end den faktiske dybde.

Det kan man bruge til at bestemme brydningsindekset for vandet: Hvis et glas vand med en mønt i bunden placeres på en overheadprojektor, kan man fokusere projektoren, så billedet af mønten står skarpt på skærmen. Men da mønten ligger på bunden af vandglasset, skal lyset passere gennemvandoverfladen, hvorved mønten ser ud til at befinde sig på en tilsyneladende dybde. Med andre ord vil projektoren ikke være stillet skarpt på et plan, der falder sammen med mønten, men i stedet i et plan der ligger lidt højere oppe i vandet.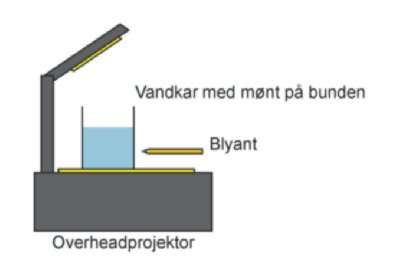

Et glas vand med en mønt i placeres på en overheadprojektor, hvorved man kan bestemme vandets brydningsindeks.

Positionen af dette plan kan bestemmes ved at køre en spids blyant op og ned langs glassets yderside, indtil billedet af blyanten på skærmen står skarpt. Når dette sker, vil blyanten befinde sig i projektorens fokuseringsplan (idet lyset fra blyanten ikke skal passerer en vand-luft overflade).

Et glas vand på en overheadprojektor. I bunden af glasset ligger en mønt, og billedet fra projektoren er fokuseret, så mønten står skarpt. En blyant køres op og ned langs siden, indtil den også står skarpt. Ud fra dette kan man bestemme vandets brydningsindeks.

Nu noteres positionen af mønten, blyanten og vandoverfladen, og man måler så op, hvor langt under vandoverfladen mønten lå (reelle dybde, L) samt hvor langt under vandoverfladen blyanten befandt sig (tilsyneladende dybde, d):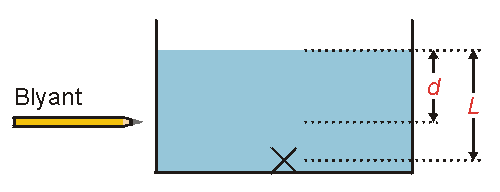

Den reelle dybde L og den tilsyneladende dybde d.

For at beregne brydningsindekset for vandet, anvender man en approksimation: Ved små vinkler er sinus til vinklen tilnærmelsesvis lig med selve vinklen. Indsættes dette i Snells Lov finder man, at brydningsindekset er lig med L / d.

Da brydningsindekset for almindeligt vand ved stuetemperatur er ca. 1,33, vil man normalt måle, at d = 0,75 x L.

Udstyr og materialer:

Vand
Stort bægerglas
Overheadprojektor
Lineal / målebånd
Blyant

Referencer:

J.F. Goehl Jr.: "Investigation of the variation of apparent depth with viewing angle by ray tracing", Am. J. Phys. 45, 999 (1977).
R.D. Edge: "Refractive index of liquids", The Physics Teacher 17, 267 (1979). (http://scitation.aip.org/tpt)
A.A. Bartlett, R. Lucero, and G.O. Johnson: "A note on a common virtual image", Am. J. Phys. 52, 640 (1984).
A. Cortel: "Apparent-Depth Demonstration Using a Plastic Box and Pins", The Physics Teacher 40, 441 (2002). (Forsøget udført med plexiglas og knappenåle.) (http://scitation.aip.org/tpt)
J.F. Goehl Jr.: "Previous Apparent-Depth Papers", The Physics Teacher 41, 4 (2003). (Kommentar til A. Cortels artikel.) (http://scitation.aip.org/tpt)

PIRA DCS: 6A40.10 (Optik: Geometrisk optik)

Opdateret: 23.11.2005

Har du kommentarer, rettelser eller tilføjelser til dette forsøg, så send en til FYSIKBASEN.DK.